To all my fellow math and comp-sci enthusiasts, let’s talk about a fascinating topic that bridges the binary world of classical computing and the mysterious universe of quantum mechanics: bits vs. qubits!

Classical Bits: Pure Black or White

Classical bits are the foundation of traditional computing—simple and straightforward. They exist in one of two states:

• 0 (pure black)
• 1 (pure white)

This is binary computing at its core. It’s as if nature decided to keep things no-nonsense here: you’re either black or white. No drama...
But you know that is not real nature – it’s so artificial and boring…

Qubits: The Spice of Quantum

Now, qubits are where things get truly exciting. Unlike classical bits, qubits aren’t limited to a single state. Instead of being just 0 or 1, qubits can exist in any combination of the two states. Mathematically speaking, qubits are vectors rather than simple scalars.

Here’s how they’re defined:

• Pure Black Qubit: |0⟩ = [1, 0]
• Pure White Qubit: |1⟩ = [0, 1]

But here’s the kicker: there’s also a magical, mysterious grey state, and not just one but millions of shades of grey! For example:

• |Ψ⟩ = [1/√2, 1/√2]
  This state is both 0 and 1 at the same time, with equal probability of being either.

Or even:

• |Ψ⟩ = [1/√2, -1/√2]
  Another unique state, with equal probability of being either, just as intriguing.

Each of these states represents a different shade of grey, depending on the amplitudes and phases. These states create a rich tapestry of possibilities, making qubits fundamentally different from classical bits.

This property of being in multiple states simultaneously is called superposition.
The moment you measure a qubit, it “collapses” into either 0 or 1.

Or, as our Kamal’s Tamil classic song in movie “Alavandaan” puts it:
😳♩ “கடவுள் பாதி, மிருகம் பாதி, கலந்து செய்த கலவை!” 😡☺
(Translation: “Half divine, half beast, a blend of the two!”)
Actually it is:
😳♩ “கடவுள் கொஞ்சம் மிருகம் கொஞ்சம், கலந்து செய்த கலவை!” 😡☺

Manipulating Bits vs. Qubits

In classical computing, bits are manipulated with basic logical operations through logic gates like:

• AND
• OR
• NOR
• NAND

It’s simple stuff. But qubits? That’s a whole different ball game. Since qubits are vectors, their manipulation involves rotations. These rotations are achieved through matrix operations, which allow us to change the direction and state of the qubit on a Bloch Sphere (a visual representation of qubit states).

The Bloch Sphere: A Visual Marvel

To add a cherry on top, let me introduce the Bloch Sphere, a conceptual tool
I delved into this back in 2018 (yes, 7 years ago!) to solidify my understanding of quantum concepts and here is my cheat sheet:-

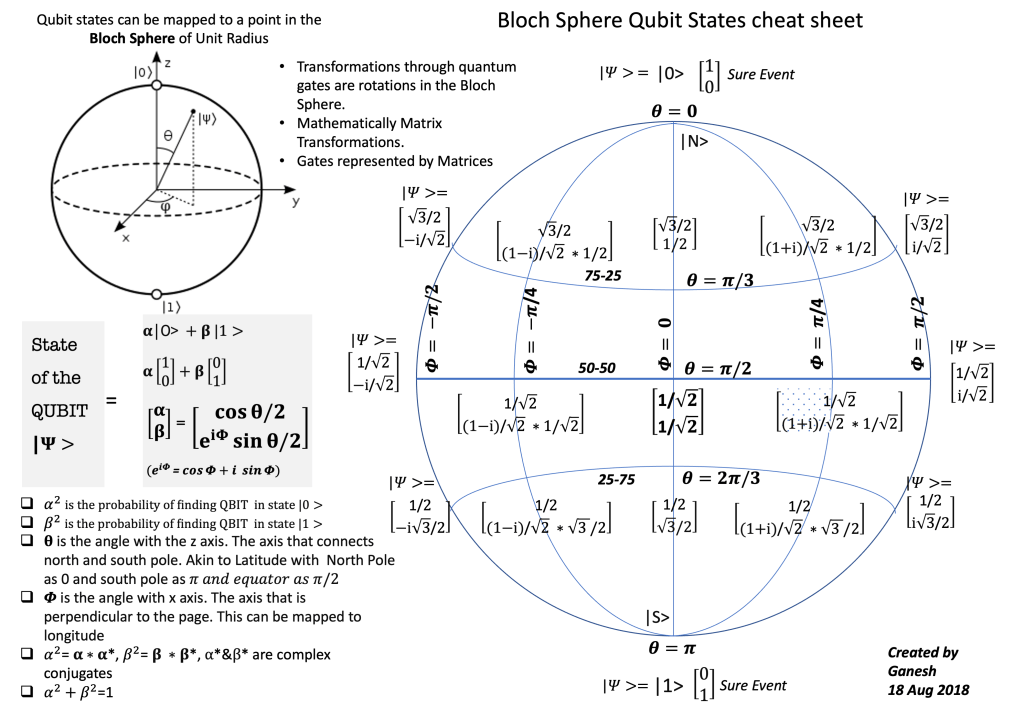
At its heart, a qubit is represented as a vector originating from the center of the Bloch Sphere and pointing to its surface. Every quantum operation or operator is essentially a rotation of this vector, executed through matrix operations.

Imagine turning a qubit’s vector around the X, Y, or Z axes to transform its state. It’s a dance of mathematics and physics that unlocks the potential for quantum computation. With every rotation, you’re exploring the infinite possibilities that lie between 0 and 1, between black and white—the millions of shades of grey.

So Reiterating – Quantum Computing Simplified

So In the Bloch Sphere, a qubit’s state is represented as a vector originating from the center and pointing to its surface. By applying rotation operators (like Pauli matrices or rotation gates), you can navigate these millions of shades of grey, moving seamlessly between superpositions and definite states.

If you have a solid grasp of Maths and Vector Algebra, you’re already halfway to understanding the basics of quantum computing. The underlying mechanics may be rooted in quantum phenomena, but the mathematical principles are as elegant as they are approachable.

For example:

• Superposition is about combining vectors.
• Measurement is about projecting these vectors onto a specific axis.
• Quantum gates are about rotating these vectors around the Bloch Sphere.

Once you view it through the lens of linear algebra, quantum computing becomes a fascinating extension of mathematics.

How Amazing is That?

Quantum computing may seem daunting at first, but at its core, it’s a beautiful blend of linear algebra, probability, and creativity. By embracing the grey states of qubits, we unlock a world of possibilities that transcend the limits of classical computation.

So, let’s keep it simple yet powerful, like mathematics itself. Let’s embrace the grey and unlock the world of quantum together!